Answer:
hello your question lacks the required figures here is the complete question
A 1.25-in diameter shaft contains a 0.25-in deep U-shaped groove that has a 1/8-in radius at the bottom of the groove. The maximum shear stress in the shaft must be limited to 12000 psi . If the shaft rotates at a constant angular speed of 6Hz , determine the maximum power that may be delivered by the shaft.
Answer: max power delivered by shaft = 4.045 hp
Step-by-step explanation:
Determine The maximum power that can be delivered by the shaft
using the given data
diameter of shaft ( D ) = 1.25 inches
depth of U-shaped groove = 0.25 inches
radius of U-shaped groove = 1/8 inches = 0.125 inches
maximum shear stress in shaft = 12000 psi
shaft angular speed at frequency of 6 Hz
firstly calculate
The minor diameter (d) = 1.25 - 2(0.25 ) = 0.5 inches
Ratio = radius of groove / minor diameter = 0.125 / 0.75 = 0.167
Ratio, = diameter of shaft / minor diameter = 1.25 / 0.75 = 1.667
k = 1.39 from stress concentration factors graph
calculate the maximum shear stress produced by the torque in the minor diameter of the shaft
Tmax =
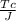 -----------equation 1
-----------equation 1
where Tc = 16T
J =
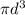
equation 1 becomes( Tmax ) =
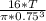
also Tmax = K * Tmin -------- equation 2
1.39 *

T ≤ 715.122 Ib-in
Tmax = 59.593 Ib-ft ( max shear stress )
Finally calculate the max power transmitted by the shaft
P max = 2
 fTmax = 2
fTmax = 2
 * 6 * 59.593
* 6 * 59.593
therefore Pmax = 2246.6 Ib-ft/s
= 4.045 hp