Answer:
Part 1
1) 0.252 kg/s
2) 457.06 K
3) 63.45%
4) 17.96 kJ
5) 44.85%
Part 2
1) 65.92 kJ
2) 57.62 kJ/kg
Step-by-step explanation:
1) The mass flow rate
The flow velocity is given by the Bernoulli relation;

Where:
ΔP = The difference in pressure = 50 - (-2) = 52 kPa
ρ = Density of air = 1.225 kg/m³
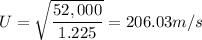
The volume flow rate, V = U × A
Where:
A = Cross sectional area of the of the inlet = 10 cm² = 0.001 m²
Therefore, V = 0.001 × 206.03 = 0.206 m³/s
The mass flow rate = ρ × V = 1.225 × 0.206 = 0.252 kg/s
2) The minimum outlet temperature
P₁v₁/T₁ = P₂v₂/T₂
v₁ = v₂
∴ P₁/T₁ = P₂/T₂
T₂ = P₂T₁/P₁ = 151.325*300/99.325 = 457.06 K
3) The isentropic efficiency no heat loss
h₁ = 300.4 kJ/kg
 = 401.3 kJ/kg
= 401.3 kJ/kg
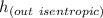 = 441.9 + (457.06 - 440)/(460 - 440)*(462.3 - 441.9) = 459.30 kJ/kg
= 441.9 + (457.06 - 440)/(460 - 440)*(462.3 - 441.9) = 459.30 kJ/kg
The isentropic efficiency,
 , is given by the expression;
, is given by the expression;
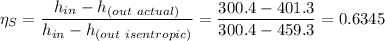
Therefore, the isentropic efficiency,
 in percentage = 63.45%
in percentage = 63.45%
4) Where there is an heat loss of 30 kJ/kg, we have;
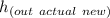 =
=
 - Heat loss = 401.3- 30 = 371.3 kJ/kg
- Heat loss = 401.3- 30 = 371.3 kJ/kg
The work done = (371.3 - 300.04)*0.252= 17.96 kJ/s
The new isentropic efficiency is given by the relation;
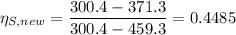
Therefore, the isentropic efficiency,
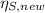 , in percentage = 44.85%
, in percentage = 44.85%
Part 2
1) Turbine mass flow rate = 0.252 kg/s
From
T₂ = P₂T₁/P₁ = 101.325*800/151.325= 535.67 K
h₁ = 822.2 kJ/kg
 = 503.3 kJ/kg
= 503.3 kJ/kg
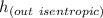 = 544.7 + (535.67 - 520)/(540 - 520)*(544.7 - 524.0) = 560.92 kJ/kg
= 544.7 + (535.67 - 520)/(540 - 520)*(544.7 - 524.0) = 560.92 kJ/kg
The maximum work,
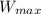 , is given by the expression;
, is given by the expression;
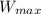 = Mass flow rate×(h₁ -
= Mass flow rate×(h₁ -
 )
)
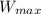 = (822 - 503.3)*0.252 = 65.92 kJ/s
= (822 - 503.3)*0.252 = 65.92 kJ/s
2) The heat lost,
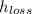 , is given by the relation;
, is given by the relation;
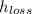 =
=
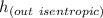 -
-
 = 560.92 - 503.3 = 57.62 kJ/kg.
= 560.92 - 503.3 = 57.62 kJ/kg.