Question

Suppose the amount of sun block lotion in plastic bottles leaving a filling machine has a normal distribution. The bottles are labeled 300 milliliters (ml) but the actual mean is 302 ml and the standard deviation is 2 ml. If you purchase a package of 6 bottles of lotion, what is closest to the probability that at least one bottle has a content

Answer 1

Question:

Suppose the amount of sun block lotion in plastic bottles leaving a filling machine has a normal distribution. The bottles are labeled 300 milliliters (ml) but the actual mean is 302 ml and the standard deviation is 2 ml. If you purchase a package of 6 bottles of lotion, what is closest to the probability that at least one bottle has a content of less than 300 ml?

Answer:

0.645314

Explanation:

Given:

Mean, u = 302

Standard deviation
`\sigma` = 2

n = 6

Let's first find P(X>300):

`Z = (X - u)/(\sigma)`

`Z = (300 - 302)/(2)`

`Z = -1`

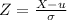
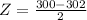
Using the standard normal table,

NORMSDIST(-1) = 0.158655

Thus,

P(Z<-1) = 0.158655

Find the closest to the probability that at least one bottle has a content of less than 300 ml:

Given that 6 bottles were purchased & p = 0.158655

Find:

P(X≥1) = 1 – P(X<1) = 1 – P(X=0)

Use bimonial distribution:

`P(X=x) = ^nC_x*p^x*(1 - p)^(^n^-^x^)`

`P(X=0) = ^6C_0* 0.158655^0*(1 - 0.158655)^(^6^-^0^)`

`P(X=0) = 1*1* 0.841345^6`

`P(X=0) = 0.354686`

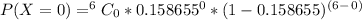
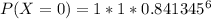
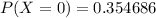
Therefore,

P(X≥1) = 1 – P(X<1) = 1 – P(X=0)

= 1 - 0.354686

= 0.645314

The closest to the probability that at least one bottle has a content of less than 300 ml is 0.645314