Question:
Suppose the amount of sun block lotion in plastic bottles leaving a filling machine has a normal distribution. The bottles are labeled 300 milliliters (ml) but the actual mean is 302 ml and the standard deviation is 2 ml. If you purchase a package of 6 bottles of lotion, what is closest to the probability that at least one bottle has a content of less than 300 ml?
Answer:
0.645314
Explanation:
Given:
Mean, u = 302
Standard deviation
 = 2
= 2
n = 6
Let's first find P(X>300):
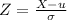
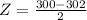
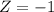
Using the standard normal table,
NORMSDIST(-1) = 0.158655
Thus,
P(Z<-1) = 0.158655
Find the closest to the probability that at least one bottle has a content of less than 300 ml:
Given that 6 bottles were purchased & p = 0.158655
Find:
P(X≥1) = 1 – P(X<1) = 1 – P(X=0)
Use bimonial distribution:

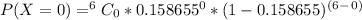
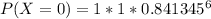
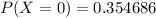
Therefore,
P(X≥1) = 1 – P(X<1) = 1 – P(X=0)
= 1 - 0.354686
= 0.645314
The closest to the probability that at least one bottle has a content of less than 300 ml is 0.645314