Answer:
2.88
Explanation:
Data provided in the question
 = Population standard deviation = 7 miles per hour
= Population standard deviation = 7 miles per hour
Random sample = n = 32 vehicles
Sample mean =
 = 64 miles per hour
= 64 miles per hour
98% confidence level
Now based on the above information, the alpha is
= 1 - confidence level
= 1 - 0.98
= 0.02
For
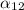 = 0.01
= 0.01
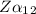 = 2.326
= 2.326
Now the margin of error is


= 2.88
hence, the margin of error is 2.88