Answer:
For the revenue per month to drop, the price per boat per month has to drop more than $2,000
Step-by-step explanation:
Given:
Number of boats sold per month = 50
Cost of each boat = $25,000
Each month demand increases at a rate of 4 boats per month.
Required:
Find the fastest price could drop before monthly revenue starts to drop.
Revenue, R = Price × Quantity
R = P × Q
Differntiate both sides with respect to time, t:
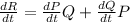
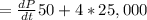
For the fastest price could drop before monthly revenue starts to drop,

Thus,
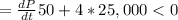
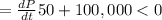
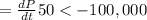
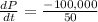
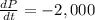
Since the answer is negative, it indicates a drop in price.
Therefore, for the revenue per month to drop, the price per boat per month has to drop more than $2,000