Question

Three trigonometric functions for a given angle are shown below. cosecant theta = thirteen-twelfths; secant theta = Negative thirteen-fifths; cotangent theta = Negative five-twelfths What are the coordinates of point (x, y) on the terminal ray of angle Theta, assuming that the values above were not simplified? (–5, 12) (5, –12) (–12, 5) (12, –5)

Answer 1

(–5, 12) is the correct answer.

Explanation:

We are given the following values:

`cosec\theta = (13)/(12)\\sec\theta=-(13)/(5)\\cot\theta =-(5)/(12)`

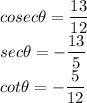
Now, we know the following identities:

`sin \theta = (1)/(cosec\theta)\\cos \theta = (1)/(sec\theta)\\tan \theta = (1)/(cot\theta)`

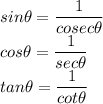
Now, the values are:

`sin\theta = (12)/(13)\\cos\theta=-(5)/(13)\\tan\theta =-(12)/(5)`

Sine value is positive and cos, tan values are negative.

It can be clearly observed that
`\theta` is in 2nd quadrant.

2nd quadrant means, the value of
`x` will be negative and
`y` will be positive.

Let us have a look at the value of
`tan\theta`:

`tan\theta = (Perpendicular)/(Base)\\OR\\tan\theta = (y-coordinate)/(x-coordinate) = -(12)/(5)\\\therefore y = 12,\\x = -5`

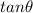Please refer to the attached image for clear understanding and detailed explanation.

Hence, the correct answer is coordinate (x,y) is (–5, 12)