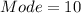Answer:
a.
i) & ii) -> See Explanation Below
a.
iii)
 and
and
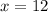
b.
i)
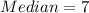
ii)
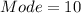
Explanation:
Given
Number of pets: 2 , 4, 6, 8, 10
Number of students: x, 2, y, 6, 14
Total students = 40
Required
a) (i) show that x+y=18
Given that total number of students is 40;
This implies that
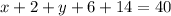
Collect like terms
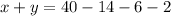
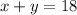
a) (ii) If the mean of the distribution is 6.4, show that x +3y =30
The mean of a distribution is calculated as thus
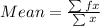
 is gotten by multiplying number of pets by corresponding number of students
is gotten by multiplying number of pets by corresponding number of students
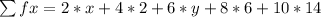
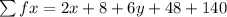
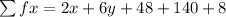
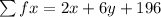
 is the total number of students
is the total number of students
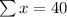
So;
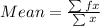 becomes
becomes
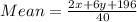
Substitute 6.4 for Mean
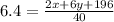
Multiply both sides by 40
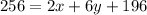
Subtract 196 from both sides
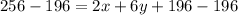
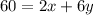
Divide both sides by 2
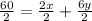
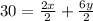

Reorder
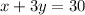
a) (iii) Hence, find the value of x and of y
Using
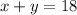 and
and
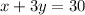
Subtract both equations
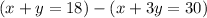
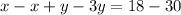
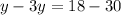
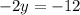
Divide both sides by -2
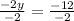
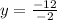

Substitute 6 for y in
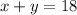
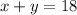 becomes
becomes
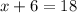
Subtract 6 from both sides
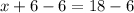
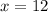
b.
i) Calculate the Median
First, we need to tabulate the given data properly
Number of Pets ------ Number of students ------- Cumulative Frequency
2 ------------------------------12 -----------------------------------12
4 ------------------------------2 -----------------------------------14
6 ------------------------------6 -----------------------------------20
8 ------------------------------6 -----------------------------------26
10 ------------------------------14 -----------------------------------40
Since the number of pets is already arranged in ascending order,
the next step is to calculate the median element
Number of students = 40
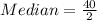
Median = 20
Given that number of students (40) is an even number,
The median is the average of the 20th and 21st element
From the table above; the median can be gotten from
6 ------------------------------6 -----------------------------------20
8 ------------------------------6 -----------------------------------26
The 20th element = 6
The 21st element = 8
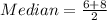
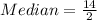
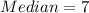
ii) Mode
The mode is the corresponding data with the highest frequency
The highest frequency is 14;
The number of pets with frequency of 14 is 10
Hence,