Answer:
The probability of tossing a tail and then rolling a number greater than 5 is 0.188
Step-by-step explanation:
Independent events:
If two events, A and B, are independent, we have that:
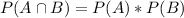
In this question:
The coin and the die are independent. So
Event A: Tossing a tail.
Event B: Rolling a number greater than 5.
Probability of tossing a tail:
Coin can be heads or tails(2 outcomes), so the probability of a tail is
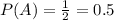
Probability of rolling a number greater than 5:
8 numbers(1 through 8), 3 of which(6,7,8) are greater than 5. So the probability of rolling a number greater than 5 is
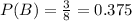
Probability of A and B:

The probability of tossing a tail and then rolling a number greater than 5 is 0.188