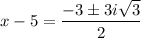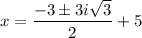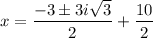2 Answers

Joergi · Answer 1 · 2021-11-29T18:54:04+0000

Answer:

$x = (7 \pm 3i√(3))/(2)$

Explanation:

(x – 5)^2 + 3(x – 5) + 9 = 0

This is a quadratic equation in x - 5.

Let u = x - 5, then the quadratic equation becomes:

u^2 + 3u + 9 = 0

We can use the quadratic formula to solve for u.

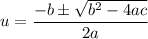
$u = (-b \pm √(b^2 - 4ac))/(2a)$

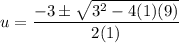
$u = (-3 \pm √(3^2 - 4(1)(9)))/(2(1))$

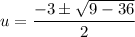
$u = (-3 \pm √(9 - 36))/(2)$

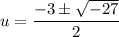
$u = (-3 \pm √(-27))/(2)$

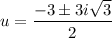
$u = (-3 \pm 3i√(3))/(2)$

Since u = x - 5, now we substitute x - 5 for u and solve for x.

$x - 5 = (-3 \pm 3i√(3))/(2)$

$x = (-3 \pm 3i√(3))/(2) + 5$

$x = (-3 \pm 3i√(3))/(2) + (10)/(2)$

$x = (7 \pm 3i√(3))/(2)$

Please log in or register to add a comment.