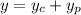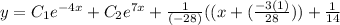Question

Write the given differential equation in the formL(y) = g(x),where L is a linear differential operator with constant coefficients. If possible, factor L. (Use D for the differential operator.)y'' − 3y' − 28y = x − 2

Answer 1

L(y) = g(x)

`y = C_(1) e^(-4 x) + C_(2) e^(7 x) + (1)/((-28))(( x + (( -3 (1) )/(28) )) + (1)/(14)`

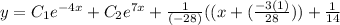
Explanation:

Step(i):-

Given differential equation

y'' − 3 y' − 28 y = x − 2

Operator form ( D² - 3 D - 28 )y = x -2

f( D ) y = Ф(x)

Auxiliary equation

f( m ) = m² - 3 m - 28

⇒ m² - 3 m - 28 =0

⇒ m² - 7 m +4 m - 28 =0

⇒ m ( m -7 ) + 4 ( m -7) =0

⇒ (m + 4)( m -7) =0

⇒ m = -4 and m =7

Complementary function

`y_(c) = C_(1) e^(-4 x) + C_(2) e^(7 x)`

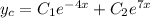
Step(ii):-

Particular integral

`P.I = y_(p) = (1)/(f(D)) (x-2)`

`= (1)/(D^(2)- 3 D - 28 ) (x)-2(1)/(D^(2) - 3 D - 28) e^(0 x) )`

`= (1)/((-28)(1 - ((D^(2)-3 D) )/(-28) )) (x) + (1)/(0-0-28) X 2`

`= (1)/((-28))( 1 + ((D^(2) -3 D) )/(28) )^(-1) (x) + (1)/(14)`

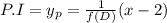
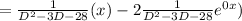
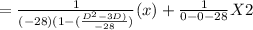
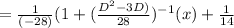
( 1 + x )⁻¹ = 1 - x + x² - x³ +.....

we use notation
`D = (dy)/(dx)`

`= (1)/((-28))( 1 + ((D^(2) -3 D) )/(28) )+ ((D^(2) -3 D) )/(28))^(2) +.....) (x) + (1)/(14)`

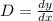
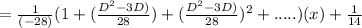
Higher degree terms will be neglected

D(x) =1

D²(x) =0

`= (1)/((-28))(( x + (( -3 (1) )/(28) )) + (1)/(14)`

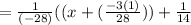
The particular integral

`y_(p) = (1)/((-28))(( x + (( -3 (1) )/(28) )) + (1)/(14)`

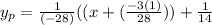
Conclusion:-

General solution of given differential equation

`y = y_(c) + y_(p)`

`y = C_(1) e^(-4 x) + C_(2) e^(7 x) + (1)/((-28))(( x + (( -3 (1) )/(28) )) + (1)/(14)`