Answer:
 , which is equal to
, which is equal to
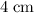 if
if
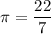 .
.
Explanation:
The surface area of a cylinder of radius
 and height
and height
 can be broken down into three parts:
can be broken down into three parts:
- two circles, one on the top and the other on the bottom, each of radius
 ;
; - a rectangle between these two circles. This rectangle shall have a width of
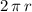 (circumference of the one such circle) and a height of
(circumference of the one such circle) and a height of
 . (Why? The height of this rectangle is the same as the distance between the top base and the bottom base of this cylinder. When the cylinder is reconstructed from these parts, that very distance becomes the height of this cylinder.)
. (Why? The height of this rectangle is the same as the distance between the top base and the bottom base of this cylinder. When the cylinder is reconstructed from these parts, that very distance becomes the height of this cylinder.)
For the cylinder in this question, it is given that diameter
 . Accordingly, the radius of this cylinder would be
. Accordingly, the radius of this cylinder would be
 .
.
The area of the two circles on the top and on the bottom, combined, should be:
![\displaystyle 2* \left(\pi\, r^2\right) = 2* \left[\left((7)/(2)\right)^2\, \pi\right] = (49)/(2)\, \pi\; \rm cm^2](https://img.qammunity.org/2021/formulas/mathematics/college/iup2nenbjx01pgoohc65uw5hz4utfdkpeq.png) .
.
Since the total surface area of this cylinder is
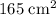 , the area of the rectangle in between would be:
, the area of the rectangle in between would be:
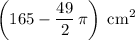 .
.
The area of a rectangle is equal to height times width. The width of this rectangle is the same as the circumference of the circle at the base:
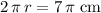 .
.
Divide the area of this rectangle by its width to find the height:
 .
.
That should be the same as the height of the cylinder.