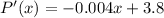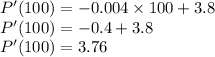Question

Let​ R(x), C(x), and​ P(x) be,​ respectively, the​ revenue, cost, and​ profit, in​ dollars, from the production and sale of x items. If ​R(x) = 6x and ​C(x) equals = 0.002x^2+2.2x+40​, find each of the following. a. p(x) b.p(100) c. P'(x) d.P'(100)

Answer 1

`a.\ P(x) = - 0.002x^2+3.8x-40`

b. 320

`c.\ P'(x) = -0.004 x + 3.8`

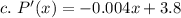
d. 3.76

Explanation:

Given that:

Revenue function:

`R(x) = 6x`

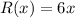
Cost Function:

`C(x) = 0.002x^2+2.2x+40`

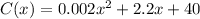
We know that,

Answer a: Profit = Revenue - Cost

`\Rightarrow P(x) = R(x) - C(x)\\\Rightarrow P(x) = 6x - (0.002x^2+2.2x+40)\\\Rightarrow P(x) = - 0.002x^2+3.8x-40`

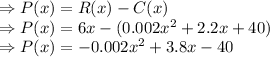
Answer b:

P(100) = ?

Putting value of x as 100 in above equation:

`P(100) = - 0.002* 100^2+3.8 * 100-40\\\Rightarrow P(100) = -20+380 -40\\\Rightarrow P(100) = 320`

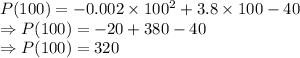
Answer c:

P'(x) = ?

Differentiating the equation
`P(x) = - 0.002x^2+3.8x-40`

`P'(x) = -2 * 0.002 x^(2-1) + 3.8 + 0\\P'(x) = -0.004 x + 3.8`

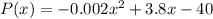
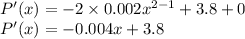
Answer d:

P'(100) = ?

Putting x = 100 in equation
`P'(x) = -0.004 x + 3.8`

`P'(100) = -0.004 * 100 + 3.8\\P'(100) = -0.4 + 3.8\\P'(100) = 3.76`