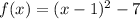Answer:
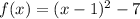 is the correct answer.
is the correct answer.
Explanation:
Given that function f(x) is:

f(x) is a quadratic function in x, meaning that it has a maximum power of 2 of x.
Vertex form of quadratic function is given as:
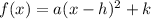
i.e. we make whole square of terms of
 .
.
Now, let us try to make whole square term of
 .
.

Adding and subtracting 1 from RHS:
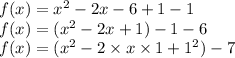
Now, using the formula:
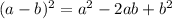
The given function becomes:
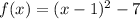
It is comparable to vertex form i.e.
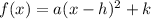
where a = 1, h = 1 and k = -7
Hence, the vertex form of given function is: