Question

When cars are equipped with flexible bumpers, they will bounce off each other during low-speed collisions, thus causing less damage. In one such accident, a 1850 kg car traveling to the right at 1.40 m/s collides with a 1450 kg car going to the left at 1.10 m/s. Measurements show that the heavier car's speed just after the collision was 0.250 m/s in its original direction.

A) What is the speed of the lighter car just after collision?
B) Calculate the change in the combined kinetic energy of the two-car system during this collision.

Answer 1

Step-by-step explanation:

Given that,

Mass of the heavier car m_1 = 1750 kg

Mass of the lighter car m_2 = 1350 kg

The speed of the lighter car just after collision can be represented as follows

`m_1u_1+m_2u_2=m_1v_1+m_2v_2\\\\v_2=(m_1u_1+m_2u_2-m_1v_1)/(m_2)`

`v_2=((1850)(1.4)+(1450)(-1.10)-(1850)(0.250))/(1450) \\\\=(2590+(-1595)-(462.5))/(1450) \\\\=(2590-1595-462.5)/(1450) \\\\=(532.5)/(1450)\\\\=0.367m/s`

b) the change in the combined kinetic energy of the two-car system during this collision

`\Delta K.E=((1)/(2) m_1v_1^2+(1)/(2) m_2v_2^2)-((1)/(2) m_1u_1^2+(1)/(2) m_2u_2^2)\\\\=(1)/(2) (m_1(v_1^2-u_1^2)+m_2(v_2^2-u_2^2))`

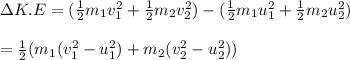
substitute the value in the equation above

`=(1)/(2) (1850((0.250)^2-(1.4)^2)+(1450((0.3670)^2-(-1.10)^2)\\\\=(1)/(2)(11850(0.0625-1.96)+(1450(0.1347)-(1.21))\\\\= (1)/(2)(11850(-1.8975))+(1450(-1.0753))\\\\=(1)/(2) (-3510.375+(-1559.185)\\\\=(1)/(2) (-5069.56)\\\\=-2534.78J`

Hence, the change in combine kinetic energy is -2534.78J