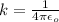Question

A dipole is oriented along the axis. The dipole moment is (Assume the center of the dipole is located at the origin with positive charge to the right and negative charge to the left.) (a) Calculate exactly the potential (relative to infinity) at a location < , 0, 0 > on the axis and at a location < 0, , 0 > on the axis, by superposition of the individual contributions to the potential. (Use the following as necessary: q, ε0, x, s and y.)

Answer 1

The potential that is as a result of the dipole at <x,0,0> is
`V_x = [(4kqs)/(4x^2 -s^2) ]`

The potential that is as a result the dipole at <0,y,0> is
`V_y = 0 volt`

Step-by-step explanation:

From the question we are told that

The dipole moment is
`p= qs`

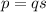
The potential at the position <x,0,0 > on the x-axis is mathematically represented as

`V_(x) = V_+ + V_-`

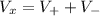
So this can be evaluated as

`V_(x) = [(kq)/(x- (s)/(2) ) ] + [(kq)/(x+ (s)/(2) ) ]`

where s is the distance between the charges

=>
`V_(x) =kq [[(1)/(x - (s)/(2) ) ] - [(1)/(x+ (s)/(2) ) ]]`

`V_x = [(4kqs)/(4x^2 -s^2) ]`

The potential at the position <0,y,0 > on the y-axis is mathematically represented as

`V_y = V_+ V_-`

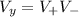
So this can be evaluated as

`V_y = [\frac{kq}{\sqrt{y^2 + ((s)/(2) )^2} } ] - [\frac{kq}{\sqrt{y^2 + ((s)/(2) )^2} } ]`

The negative sign shows that the potential value right side of the minus sign is a negative potential

`V_y = 0 volt`

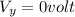
Note
`k = (1)/(4 \pi \epsilon _o )`