Question

Use the graph to complete the statement. O is the origin. Ry−axis ο Ry=x: (2,3)

Answer 1

-3,2

Explanation:

Answer 2

The complete statement is
`(R_(y-axis) \circ R_(y=x)) (2, 3) = (-3, 2)`

Explanation:

Given that we have a composition transformation where the operation R stands for reflection, we are to start from the right operation then we work on the left as follows

`(R_(y-axis) \circ R_(y=x)) (2, 3)`

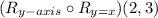
The reflection of a point (x, y) cross the line y = x is (y, x)

Therefore, when (2, 3) is reflected across the line y = x it becomes (3, 2)

The next operation, which is the reflection across the line y = x is then found as follows;

The reflection of a point (x, y) cross the y-axis is (-x, y)

Therefore, when (3, 2) is reflected across the y-axis it becomes (-3, 2)

Therefore, the complete statement is
`(R_(y-axis) \circ R_(y=x)) (2, 3) = (-3, 2)`