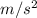Answer:
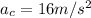
Explanation:
the centripetal acceleration is defined by the following formula:
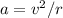
where v is the tangential velocity, and r is the radius.
if we have an acceleration of
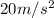 and a radius of 4m the equation becomes:
and a radius of 4m the equation becomes:
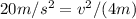
and from here we can find the tangential velocity of the object:
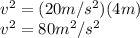
we can use this quantity to find the centripetal acceleration when the radius is 5m.
Again using the centripetal acceleration formula:
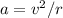
we substitute
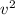 and
and
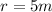 :
:
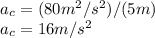
the centripetal acceleration is 16