Answer:
y = 1
Explanation:
Given:
- equation of the parabola:

- points on the parabola: (-1, -9) and (1, 1)
Substitute point (1, 1) into the given equation of the parabola to find q:
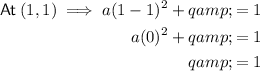
Substitute the found value of q and point (-1, -9) into the given equation of the parabola to find a:
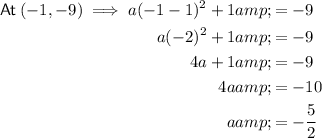
Therefore, the equation of the parabola is:
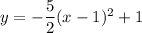
The maximum or minimum point on a parabola is the vertex.
Vertex form of a parabola:
 where (h, k) is the vertex.
where (h, k) is the vertex.
Therefore, the vertex of the parabola is (1, 1) and so the maximum value of y = 1