Question

Find all the second order partial derivatives of g (x,y) = x Superscript 4 Baseline y + 3 sine (y) + 5 y cosine (x)

Answer 1

Explanation:

Given the function
`g(x,y) = x^(4)y+3siny+5ycosx`

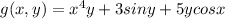
before we can get its second order partial derivative, we need to get its first order first. The first order are δg/δx and δg/δy

δg/δx
`= 4x^(3)y - 5ysinx`

δg/δy =
`x^(4) +3cosy+5cosx`

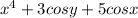
The second derivatives are δ²g/δy², δ²g/δx², δ²g/ δyδx or δ²g/ δxδy

δ²g/δy² = δ/δy (δg/δy) = δ/δy(
`x^(4)+3cosy+5cosx`)

δ²g/δy² = -3siny

Similarly δ²g/δx² = δ/δx (δg/δx) = δ/δx(
`4x^(3)y - 5ysinx`)

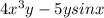δ²g/δx² = 12x²y-5ycosx

δ²g/ δyδx = δ/δy (δg/δx) = δ/δy (
`4x^(3)y - 5ysinx`)

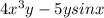δ²g/ δyδx = 4x³ - 5sinx = δ²g/ δxδy ( for continuous function)