Answer:

Explanation:
We are given the coordinates of points P(1,-6,7) and Q(-9,10,-5).
The values in the form of (
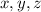 ) are:
) are:
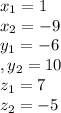
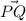 can be written as the difference of values of x, y and z axis of the two points i.e. change in axis.
can be written as the difference of values of x, y and z axis of the two points i.e. change in axis.
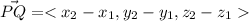
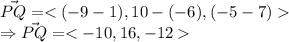
The equation of line in vector form can be written as:
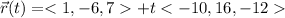
The standard parametric equation can be written as:
