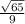Question

What is the value of sin teta if sec teta =-9/4 and teta is in the second quadrant ​

Answer 1

sin θ =
`(√(65) )/(9)`.

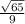Explanation:

Remember that:

sec θ is the reciprocal of cos θ. Therefore:

cos θ = -4/9.

From this, we can derive that:

Adjacent side = -4.

Hypotenuse = 9

Use the Pythagorean Theorem to solve for the 'Opposite' side:

9² = (-4)² + b²

81 = 16 + b²

65 = b²

b = √65

sin θ = O/H, so:

sin θ =
`(√(65) )/(9)`

Answer 2

Sin θ = √65/9

Explanation:

Sec θ = -9/4

Sec θ = hypotenuse/base

So, hyp = 9, base = -4

Using Pythagorean Theorem to find perp

81 = 16 + P²

P² = √65

Now

Sin θ = Perp/Hyp

Sin θ = √65/9