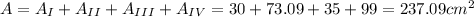Answer:
Total area = 237.09

Explanation:
Area of equilateral triangle is given as:
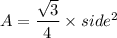
 is equilateral triangle with side = 13 cm
is equilateral triangle with side = 13 cm
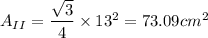
Side EA = ED + DA
CDEF is a rectangle, so CF = ED
EA = CF+DA
19=7+DA
DA = 12 cm
Looking in the region I, i.e. right angle
 .
.
According to pythagoras theorem:
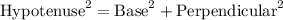
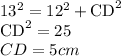
Area of a right angled Triangle:
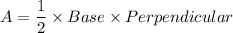
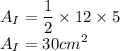
Area of rectangle is given as: Length
 Width
Width
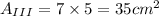
For finding area of trapezium i.e. region IV, let us draw a line parallel to side FG at E that will cut GH at a point P and 'h' is the height of triangle or distance between parallel sides of trapezium.
Now, we have a triangle EPH whose 3 sides are given as a=12, b=9 and c=15.
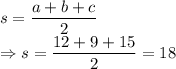
Using hero's formula for area of a triangle:
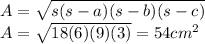
Comparing with:
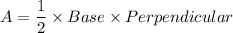
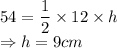
h is distance between parallel sides of trapezium.
Area of trapezium:

Total area =