Answer:
The correct answer is
.
Explanation:
Method #1: Converting the given fraction to a decimal
If we convert
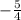to a decimal, we will get
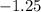. We can then see that we only need to add
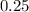to obtain our final needed value of
.
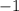The mathematical process that I used to find this answer is shown here (of course, you may have learned another way than I have adapted to - if this is the case, please stick with the method that you know for adding and subtracting decimals!):
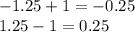
I always use the operation that I showed above to obtain my values. This may not work for you, and that is perfectly okay. Adding and subtracting decimals can be very tedious, but it comes as an easier obstacle throughout practice and time.
Method #2: Converting all integers to fractions
This method is much easier to use because the math is laid out for you in a more organized way.
To start, integers are any whole number that is not a fraction (they can be positive or negative). So, our value of
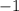qualifies as an integer.
Together, we are going to convert this value to a fraction in order to obtain fractions for ALL of our values and figure out what fraction we need in order to fulfill the requirements of our question.
To start, we already have
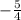in fraction form. We need to convert
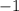to a fraction. This is really easy to do. To transform a whole number to a fraction, follow these steps:
→ 1. If the number is negative, install the negative sign in front of the fraction. If the number is positive, you may ignore this step (fractions without a leading operation sign are always inferred to be positive without the sign).
→ 2. The numerator and the denominator will be the same value as the integer (i.e., if the integer is
, the simplified fractional form is always going to be
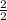- you can use multiples of the numerator to obtain unsimplified versions of the fraction, but it is best to keep it simplified to make our operations much easier to deal with).
With this information, we can convert
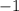to
.
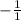Now, we need to find a least common multiple so that our denominators can be equal to each other and make our operations even easier to work with (once you see these steps multiple times with your own practice, you will be able to see how easy it is to do without it - just like stated earlier, this skill comes with time and much more math to come).
The denominator of
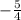is
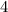. We need to get the denominator of
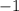equivalent to follow these steps:
→ 1. Figure out what the fractional form of the denominator is (i.e., if the denominator of a fraction is
, that value has a fractional form of
).
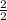→ 2. Now, multiply the value that you get from completing the previous step by the newly converted fraction to get the common denominator and easier operations.
Using these steps, we now convert the newly converted fraction
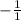to
.
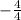Here's the math worked out for this step:
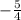has a denominator of 4 - get the fractional form of this value:
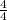
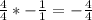
Finally, we can now figure out what we need to add to
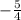to get
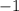. To do this, we are going to use the keep-change-change (KCC) shortcut to solve this much quicker (this is the only way that I will demonstrate because the other way is just a reciprocal operation). I will show the math for this step below:
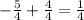
Knowing that we have two different values that we have solved for (one in decimal form and one in fractional form), we can see that they are equivalent to each other and therefore have both options as final answers depending on the demanded format for submission.
I hope this is very helpful. If anything is unclear, please let me know so I may clear it up! Best of luck!