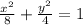Answer:
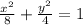
Explanation:
The directrices in this case are vertical lines, so we have a horizontal ellipse. The equation for that ellipse is:
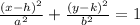
The center of the ellipse is (h,k), the diretrix is x = d and the foci are given by (h+c, k) and (h-c, k)
So, comparing the foci, we have that k = 0 and:
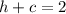
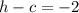
Adding these two equations, we have:
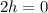
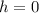
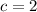
We can find the value of a^2 using the property:
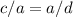
Using c = 2 and d = 4, we have:
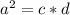
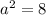
Now, to find b^2, we use the property:
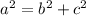
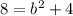
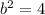
So the equation of the ellipse is: