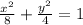Question

Which is equation of an ellipse of an ellipse with directrices at x=4 and foci at (2,0) (-2,0)

Answer 1

`(x^2)/(8) + (y^2)/(4)=1`

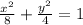
Explanation:

The directrices in this case are vertical lines, so we have a horizontal ellipse. The equation for that ellipse is:

`((x - h)^2)/(a^2) + ((y-k)^2)/(b^2)=1`

The center of the ellipse is (h,k), the diretrix is x = d and the foci are given by (h+c, k) and (h-c, k)

So, comparing the foci, we have that k = 0 and:

`h + c = 2`

`h - c = -2`

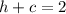
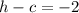
Adding these two equations, we have:

`2h = 0`

`h = 0`

`c = 2`

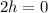
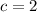
We can find the value of a^2 using the property:

`c / a = a / d`

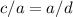
Using c = 2 and d = 4, we have:

`a^2 = c * d`

`a^2 = 8`

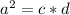
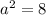
Now, to find b^2, we use the property:

`a^2 = b^2 + c^2`

`8 = b^2 + 4`

`b^2 = 4`

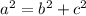
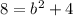
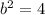
So the equation of the ellipse is:

`(x^2)/(8) + (y^2)/(4)=1`