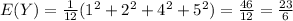Answer:
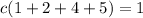
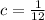
Now we can find the expected value with this formula:
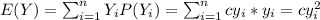
And replacing we got:
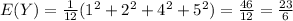
Explanation:
For this case we know the following probability mass function given:
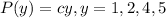
For this case we need to satisfy the following condition in order to have a probability distribution function:
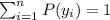
And we have this:
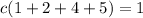
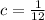
Now we can find the expected value with this formula:
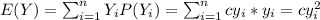
And replacing we got: