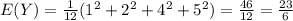Question

A probability distribution for a random variable Y is given by P(Y=y)=cy, for y=1,2,4,5 and c is a constant. Find E(Y), the expected value of Y. Give your answer as a fraction in its simplest form.

Answer 1

`c(1+2+4+5) =1`

`c =(1)/(12)`

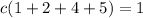
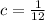
Now we can find the expected value with this formula:

`E(Y) =\sum_(i=1)^n Y_i P(Y_i) =\sum_(i=1)^n cy_i *y_i = cy^2_i`

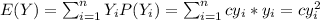
And replacing we got:

`E(Y) = (1)/(12) (1^2 + 2^2 + 4^2 +5^2) = (46)/(12)= (23)/(6)`

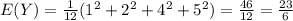
Explanation:

For this case we know the following probability mass function given:

`P(y) = cy , y= 1,2,4,5`

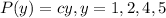
For this case we need to satisfy the following condition in order to have a probability distribution function:

`\sum_(i=1)^n P(y_i) =1`

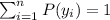
And we have this:

`c(1+2+4+5) =1`

`c =(1)/(12)`

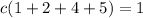
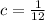
Now we can find the expected value with this formula:

`E(Y) =\sum_(i=1)^n Y_i P(Y_i) =\sum_(i=1)^n cy_i *y_i = cy^2_i`

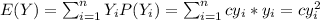
And replacing we got:

`E(Y) = (1)/(12) (1^2 + 2^2 + 4^2 +5^2) = (46)/(12)= (23)/(6)`