Answer:
(A) AA Similarity Theorem
Explanation:
Given: AB ∥ DE
To Prove:
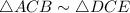
Given Triangle ABC with Line DE drawn inside of the triangle and parallel to side AB. The line DE forms a new triangle DCE.
Because AB∥DE and segment CB crosses both lines, we can consider segment CB a transversal of the parallel lines.
Angles CED and CBA are corresponding angles of transversal CB and are therefore congruent, so ∠CED ≅ ∠CBA.
We can state ∠C ≅ ∠C using the reflexive property.
Therefore,
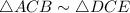 by the AA similarity theorem.
by the AA similarity theorem.
Remark: In the diagram, we can see that the two triangles share Angle C and have two equal angles at E and B. Therefore, they are similar by the Angle-Angle Similarity Theorem.