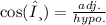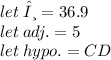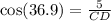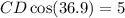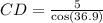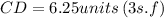Question

What is the length, in units, of segment CD?

Answer 1

The answet is C.

Explanation:

First, you have to find the angle of ACB using Sine Rule, sinθ = opposite/hypotenuse :

`\sin(θ ) = (oppo.)/(hypo.)`

`let \: oppo. = 4 \\ let \: hypo. = 5`

`\sin(θ) = (4)/(5)`

`θ = {\sin( (4)/(5) ) }^( - 1)`

`θ = 53.1 \: (1d.p)`

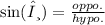
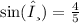
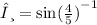
Given that line AB is parallel to line CD so ∠C = 90°. Next, you have to find the angle of ACD :

`ACD = 90 - 53.1 = 36.9`

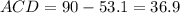
Lastly, you can find the length of CD using Cosine rule, cosθ = adjacent/hypotenuse :

`\cos(θ) = (adj.)/(hypo.)`

`let \: θ = 36.9 \\ let \: adj. = 5 \\ let \: hypo. = CD`

`\cos(36.9 ) = (5)/(CD)`

`CD \cos(36.9) = 5`

`CD = (5)/( \cos(36.9) )`

`CD = 6.25 units\: (3s.f)`