Question

Find the value of y Log^2 32=y

Answer 1

Explanation:

First of all, I have a strong feeling that that is supposed to be

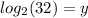`log_2(32)=y` so I'm going to go with that. We can solve for y by rewriting that in exponential form. Exponential form and log form are inverses of each other. If the log form of an equation is

`log_b(x)=y`, the exponential form of it is

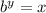`b^y=x`. We will apply that here to solve for y:

`2^y=32`

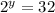
which is asking us, "2 to the power of what equals 32?". We can use our calculator to raise 2 to consecutive powers til we reach the one that gives us a 32, or we could solve it by writing the 32 in terms of a 2:

`2^y=2^5`

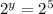
Since both bases are the same, 2, then the exponents are equal to one another. y = 5. This is an important rule to remember while solving either log or exponential equations.