Question

A triangle is rotated 90° about the origin. Which rule describes the transformation?

O(,y) - (x, y)
(x,y) - (y,x)
(x,y) - (y; -)
O(x, y) - (y;-)

Answer 1

(x, y) - (y, -x)

Explanation:

Rotation is a process in which the orientation of a given figure is changed by turning it about a point called origin. The rotation can be done either clock-wisely or counterclockwise about the origin.

If the given triangle is rotated
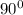`90^(0)` clockwise, the rule that describe the transformation is; (x, y) - (y, -x)

If the given triangle is rotated
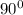`90^(0)` counterclockwise, the rule that describe the transformation is; (x, y) - (-y, x)

In the given question, the required rule is; (x, y) - (y, -x). This shows a clockwise rotation of
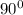`90^(0)` about the origin.