Answer:
The probability is 0.1304 = 13.04%.
Explanation:
For each adult, there are only two possible outcomes. Either they use their smartphone in meetings or classes, or they do not. The probability of an adult using their smartphone in meetings or classes is independent of other adults. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
54% use them in meetings or classes.
This means that
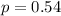
If 15 adult smartphone users are randomly selected, find the probability that exactly 10 of them use their smartphones in meetings or classes.
This is P(X = 10) when n = 15. So

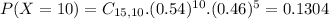
The probability is 0.1304 = 13.04%.