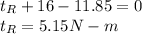Answer:
a) Check definition below
b) Number of teeth in the sun gear is 30
c) The sketch is in the attached file
d) The output torque is 11.85 Nm
e) The torque that must be applied to the ring to keep it stationary is 5.15 Nm
Step-by-step explanation:
a) Circular pitch is the ratio of the circumference of the pitch circle to the number of teeth contained in the gear.
It is given by the relationship,
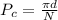
Where N is the number of teeth in the gear and d is the diameter of the pitch.
b) The relationship between the number of teeth in the sun gear, ring gear and planet gear can be given as:

Number of teeth in ring gear,
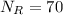
Number of teeth in the planet gear,
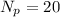
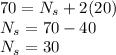
Number of teeth in the sun gear is 30
c) The sketch of the forces applied to the arm and gear is attached as a file below
d)
The speed of rotation of the sun gear,
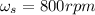
torque on the sun gear,

We can get the output torque of the planet gear by assuming an efficiency of 100%, where the input power will equal the output power.
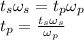
To calculate the rotational speed of the planet,
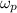 , first calculate the rotational speed of the arm,
, first calculate the rotational speed of the arm,
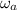 using the relation below:
using the relation below:
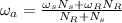
The rotational speed of the ring gear is 0,
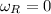

Then calculate the rotational speed of the planet from the relation below:

The output torque is then calculated from the relation below:
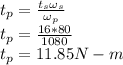
The torque output = 11.85 N-m
e)
For equilibrium, Summation of the torques applied on the gear is zero
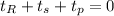
The torque applied on the planet is applied anti-clockwisely,