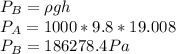Note: The drawing referred to in the question is attached below
Answer:
gauge pressure that the water has at the faucet in house A = 254878.4 Pa
gauge pressure that the water has at the faucet in house B = 186278.4 Pa
Step-by-step explanation:
Mass of water,
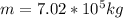
Calculate the volume of water in the reservoir:
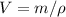
Where
 = density of water = 10³ kg/
= density of water = 10³ kg/
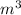
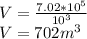
Since the reservoir is spherical in shape, the volume of a sphere is given by the equation:
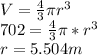
By observing the diagram shown, the height of the tower to house A:
h = 2r + 15 = 2(5.504) + 15 = 26.008 m
The gauge pressure in house A can be given by the formula:
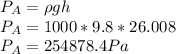
By observing the diagram shown, the height of the tower to house B:
h = 2r + 15 - 7 = 2(5.504) + 15 - 7
h= 19.008 m