Answer:
0.25 feet per minute
Explanation:
Gravel is being dumped from a conveyor belt at a rate of 20 ft3/min. Since we are told that the shape formed is a cone, the rate of change of the volume of the cone.
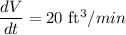
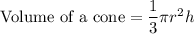
Since base diameter = Height of the Cone
Radius of the Cone = h/2
Therefore,

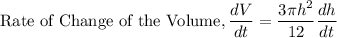
Therefore:
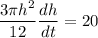
We want to determine how fast is the height of the pile is increasing when the pile is 10 feet high.

When the pile is 10 feet high, the height of the pile is increasing at a rate of 0.25 feet per minute