Answer:
1) 34 + 0i
2) 9/17 + (2/12)i
3) z = -i
Explanation:
Part 1:
(5 + 3i)(5 - 3i) = 25 - 15i + 15i - 9i²
25 - 15i + 15i - 9i² = 25 - 9i²
25 - 9i² = 25 - 9√(-1)²
25 - 9√(-1)² = 25 - 9(-1)
25 - 9(-1) = 25 + 9
25 + 9 = 34
34 = 34 + 0i
Part 2:
(2 + i) / (4 + i)
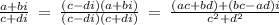
a=2, b= 1 , c=4 , d =1
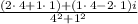
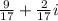
Part 3:
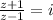
Solve like part 2:
z = -i