Question

1. Compute (5+3i)(5-3i)

express your answer in the form of a+bi, where a and b are real numbers.

2. Express (2+i)/(4+i) in the form of a+bi, where a and b are real numbers.

3. Find all complex number z satisfying the equation (z+1)/(z-1)=i


THANKS SO MUCH FOR YOUR HELP!!!

Answer 1

1) 34 + 0i

2) 9/17 + (2/12)i

3) z = -i

Explanation:

Part 1:

(5 + 3i)(5 - 3i) = 25 - 15i + 15i - 9i²

25 - 15i + 15i - 9i² = 25 - 9i²

25 - 9i² = 25 - 9√(-1)²

25 - 9√(-1)² = 25 - 9(-1)

25 - 9(-1) = 25 + 9

25 + 9 = 34

34 = 34 + 0i

Part 2:

(2 + i) / (4 + i)

`(a+bi)/(c+di)\:=\:(\left(c-di\right)\left(a+bi\right))/(\left(c-di\right)\left(c+di\right))\:=\:(\left(ac+bd\right)+\left(bc-ad\right)i)/(c^2+d^2)`

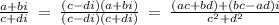
a=2, b= 1 , c=4 , d =1

`(\left(2\cdot \:4+1\cdot \:1\right)+\left(1\cdot \:4-2\cdot \:1\right)i)/(4^2+1^2)`

`(9)/(17)+(2)/(17)i`

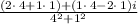
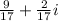
Part 3:

`(z+1)/(z-1)=i\\`

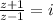
Solve like part 2:

z = -i