Answer:
Explanation:
given the differential equation x^4(dy/dx) +x^3y =- sec (xy). Solving using the variable separable method;
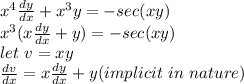
Substituting v and dv/dx into the equation above we have;
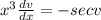
Separating the variables:
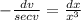
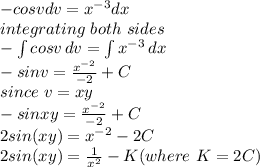
The final expression gives the solution to the differential equation.