Question

1. X^4(dy/dx) +x^3y =- sec (xy)

Integral by separation of variables?
​

Answer 1

Explanation:

given the differential equation x^4(dy/dx) +x^3y =- sec (xy). Solving using the variable separable method;

`x^(4) (dy)/(dx) +x^(3)y = -sec(xy)\\x^(3)(x(dy)/(dx) + y) = -sec(xy)\\let \ v=xy\\(dv)/(dx) = x(dy)/(dx) + y(implicit \ in\ nature)\\`

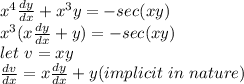
Substituting v and dv/dx into the equation above we have;

`x^(3)(dv)/(dx) = -secv`

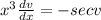
Separating the variables:

`-(dv)/(secv) = (dx)/(x^(3) )`

`-cosvdv = x^(-3)dx\\ integrating\ both\ sides\\-\int\limits {cosv} \, dv = \int\limits {x^(-3) } \, dx\\-sinv = (x^(-2) )/(-2) + C\\since\ v = xy\\-sinxy = (x^(-2) )/(-2) + C\\2sin(xy) = x^(-2) -2C\\2 sin(xy) = (1)/(x^(2) ) -K (where\ K = 2C)\\`

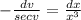
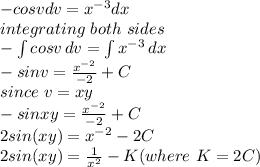
The final expression gives the solution to the differential equation.