Answer:
It is therefore not possible to insure and earn interest on $7500
Step-by-step explanation:
Total amount deposited is $100.000 in to finance institutions given FinA and Fin B
FinA pays 8% on only deposits insured to $50.000
FinB pays 6.4% on only deposits insured to $100.00
To determine if the money can be deposited we to ain an interest of $7500
Let $x be amount deposited in FinA and $(100.000-x) be the amount deposited in FinB.
x
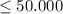 thus we cant insure full amount
thus we cant insure full amount
Annual interest is $[(8/100*x)+(6.4/100*(100.000-x))
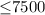
= (2/125*x+640)
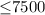
Thus since x
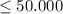
(2/125*x)
 (2/125*50.000)
(2/125*50.000)
(2/125*x)
 8
8