Answer:
The friction factor of a 60-mm-diameter galvanized iron pipe is 0.045.
Step-by-step explanation:
Losses due to friction flowing through iron pipe is determined by the Darcy-Weisbach model:

Where:
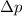 - Pressure drop, measured in pascals.
- Pressure drop, measured in pascals.
 - Density of water, measured in kilograms per cubic meter.
- Density of water, measured in kilograms per cubic meter.
 - Friction factor, dimensionless.
- Friction factor, dimensionless.
 - Length of the pipe, measured in meters.
- Length of the pipe, measured in meters.
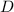 - Diameter of the pipe, measured in meters.
- Diameter of the pipe, measured in meters.
 - Velocity of the flow, measured in meters per second.
- Velocity of the flow, measured in meters per second.
The friction factor is now cleared:

The flow velocity is equal to the volume flow divided by the cross area of the iron pipe. That is:
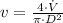
Given that
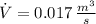 and
and
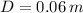 , the velocity of the flow is:
, the velocity of the flow is:


Now, if
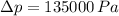 ,
,
 and
and
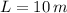 . The friction factor is:
. The friction factor is:
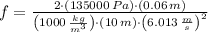
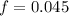
The friction factor of a 60-mm-diameter galvanized iron pipe is 0.045.