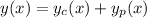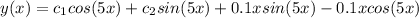Question

Solve the nonhomogeneous differential equation y′′+25y=cos(5x)+sin(5x). Find the most general solution to the associated homogeneous differential equation. Use c1 and c2 in your answer to denote arbitrary constants. Enter c1 as c1 and c2 as c2.

Answer 1

`y(x)=c_1cos(5x)+c_2sin(5x)+0.1xsin(5x)-0.1xcos(5x)`

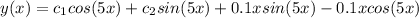
Explanation:

The general solution will be the sum of the complementary solution and the particular solution:

`y(x)=y_c(x)+y_p(x)`

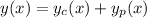
In order to find the complementary solution you need to solve:

`y''+25y=0`

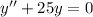
Using the characteristic equation, we may have three cases:

Real roots:

`y(x)=c_1e^(r_1x) +c_2e^(r_2x)`

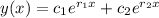
Repeated roots:

`y(x)=c_1e^(rx) +c_2xe^(rx)`

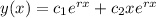
Complex roots:

`y(x)=c_1e^(\lambda x)cos(\mu x) +c_2e^(\lambda x)sin(\mu x)\\\\Where:\\\\r_1_,_2=\lambda \pm \mu i`

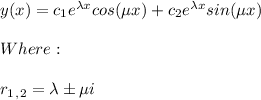
Hence:

`r^(2) +25=0`

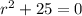
Solving for
`r` :

`r=\pm5i`

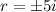
Since we got complex roots, the complementary solution will be given by:

`y_c(x)=c_1cos(5x)+c_2sin(5x)`

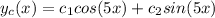
Now using undetermined coefficients, the particular solution is of the form:

`y_p=x(a_1cos(5x)+a_2sin(5x) )`

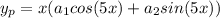
Note:
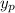`y_p` was multiplied by x to account for
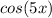`cos(5x)` and
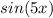`sin(5x)` in the complementary solution.

Find the second derivative of
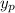`y_p` in order to find the constants
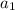`a_1` and
`a_2` :

`y_p''(x)=10a_2cos(5x)-25a_1xcos(5x)-10a_1sin(5x)-25a_2xsin(5x)`

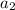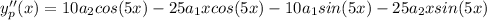
Substitute the particular solution into the differential equation:

`10a_2cos(5x)-25a_1xcos(5x)-10a_1sin(5x)-25a_2xsin(5x)+25(a_1xcos(5x)+a_2xsin(5x))=cos(5x)+sin(5x)`

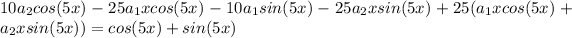
Simplifying:

`10a_2cos(5x)-10a_1sin(5x)=cos(5x)+sin(5x)`

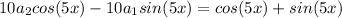
Equate the coefficients of
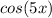`cos(5x)` and
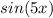`sin(5x)` on both sides of the equation:

`10a_2=1\\\\-10a_1=1`

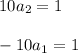
So:

`a_2=(1)/(10) =0.1\\\\a_1=-(1)/(10) =-0.1`

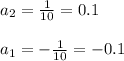
Substitute the value of the constants into the particular equation:

`y_p(x)=-0.1xa_1cos(5x)+0.1xsin(5x)`

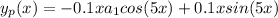
Therefore, the general solution is:

`y(x)=y_c(x)+y_p(x)`

`y(x)=c_1cos(5x)+c_2sin(5x)+0.1xsin(5x)-0.1xcos(5x)`