Answer:
The smallest radius at the junction between the cross section that can be used to transmit the torque is 0.167 inches.
Step-by-step explanation:
Torsional shear stress is determined by the following expression:
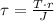
Where:
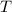 - Torque, measured in
- Torque, measured in
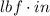 .
.
 - Radius of the cross section, measured in inches.
- Radius of the cross section, measured in inches.
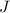 - Torsion module, measured in quartic inches.
- Torsion module, measured in quartic inches.
 - Torsional shear stress, measured in pounds per square inch.
- Torsional shear stress, measured in pounds per square inch.
The radius of the cross section and torsion module are, respectively:
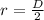
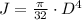
Where
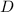 is the diameter of the cross section, measured in inches.
is the diameter of the cross section, measured in inches.
Then, the shear stress formula is now expanded and simplified as a function of the cross section diameter:
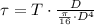
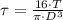
In addition, diameter is cleared:
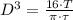
![D = 2\cdot \sqrt[3] {\frac {2\cdot T}{\pi\cdot \tau}}](https://img.qammunity.org/2021/formulas/engineering/college/830u3zxk10ru6l2t66upgiwrvivh0kmhyw.png)
If
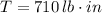 and
and
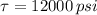 , then:
, then:
![D = \sqrt[3]{(2\cdot (710\,lbf\cdot in))/(\pi \cdot (12000\,psi)) }](https://img.qammunity.org/2021/formulas/engineering/college/6rddlnqoobytm1vgbychqy5a7k943gt17k.png)
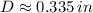
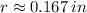
The smallest radius at the junction between the cross section that can be used to transmit the torque is 0.167 inches.