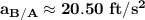Answer:
the acceleration of the wedge
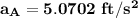
the acceleration of the block relative to the wedge is
Step-by-step explanation:
Let assume that the angle at which the block starts to slide is 30°
Given that ;
the weight of block B =
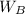 = 12-lb
= 12-lb
the weight of wedge A =
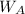 = 30-lb
= 30-lb
The 12-lb block B starts from rest and slides on the 30-lb wedge A, which is supported by a horizontal surface.
We can resolve the equation of motion for the wedge and the block into the vertical component and horizontal components as follows:
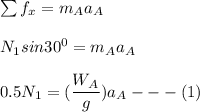
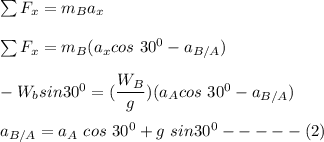
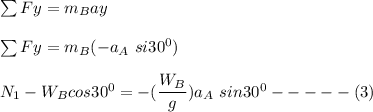
From equation (1)
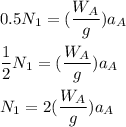
From equation (3) ; we have:
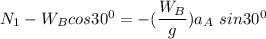
replacing
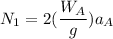 in above equation (3); we have :
in above equation (3); we have :
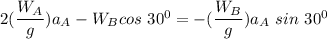
Making
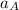 the subject of the formula; we have :
the subject of the formula; we have :
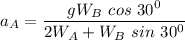
where ; g =
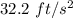
the weight of block B =
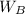 = 12-lb
= 12-lb
the weight of wedge A =
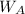 = 30-lb
= 30-lb
Solving for the acceleration of wedge A
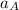 ; we have;
; we have;
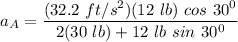
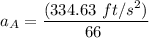
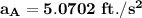
Thus; the acceleration of the wedge
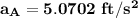
To determine the acceleration of the block relative to the wedge
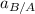 ; Let consider equation 2
; Let consider equation 2
From equation 2;
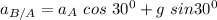
we know that:
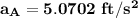
g = 32.2 ft/s²
Thus;
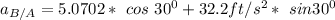
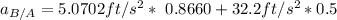
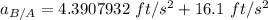
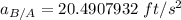
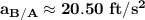
Thus; the acceleration of the block relative to the wedge is