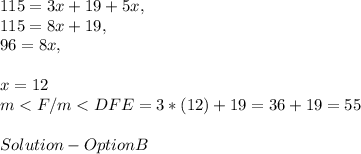Answer:
Option B
Explanation:
Angle SDE is an exterior angle. This question can be solved it two ways;
1. Find the m∠ FDE through the definition of Linear Pair, subtracting 115 from 180, and then through the ∑ of ∠s in Δ Theorem, solve for the value of x. Substitute into " 3x + 19 " and solve for the measure of DFE.
2. Apply the Exterior Angles Theorem and make m∠ SDE ( Exterior Angle ) equivalent to the sum of it's remote interior angles DFE and DEF. Given their measures to be 3x + 19 and 5x, we can solve for the value of x. Substitute into " 3x + 19 " and solve for the measure of DFE.
For the simplicity, I would consider the second option;