Answer:
(a) Fw = 101.01 N
(b) W = 282.82 J
(c) Fg = 382.2 N
(d) N = 368.61 N
(e) Net force = 0 N
Step-by-step explanation:
(a) In order to calculate the magnitude of the worker's force, you take into account that if the ice block slides down with a constant speed, the sum of forces, gravitational force and work's force, must be equal to zero, as follow:
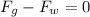 (1)
(1)
Fg: gravitational force over the object
Fw: worker's force
However, in an incline you have that the gravitational force on the object, due to its weight, is given by:
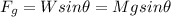 (2)
(2)
M: mass of the ice block = 39 kg
g: gravitational constant = 9.8m/s^2
θ: angle of the incline
You calculate the angle by using the information about the distance of the incline and its height, as follow:
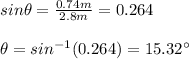
Finally, you solve the equation (1) for Fw and replace the values of all parameters:
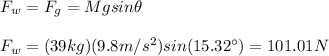
The worker's force is 101.01N
(b) The work done by the worker is given by:
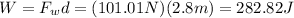
(c) The gravitational force on the block is, without taking into account the rotated system for the incline, only the weight of the ice block:
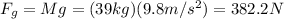
The gravitational force is 382.2N
(d) The normal force is:
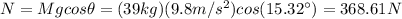
(e) The speed of the block when it slides down the incle is constant, then, by the Newton second law you can conclude that the net force is zero.