Question

A 39 kg block of ice slides down a frictionless incline 2.8 m along the diagonal and 0.74 m high. A worker pushes up against the ice, parallel to the incline, so that the block slides down at constant speed. (a) Find the magnitude of the worker's force. How much work is done on the block by (b) the worker's force, (c) the gravitational force on the block, (d) the normal force on the block from the surface of the incline, and (e) the net force on the block?

Answer 1

(a) Fw = 101.01 N

(b) W = 282.82 J

(c) Fg = 382.2 N

(d) N = 368.61 N

(e) Net force = 0 N

Step-by-step explanation:

(a) In order to calculate the magnitude of the worker's force, you take into account that if the ice block slides down with a constant speed, the sum of forces, gravitational force and work's force, must be equal to zero, as follow:

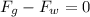`F_g-F_w=0` (1)

Fg: gravitational force over the object

Fw: worker's force

However, in an incline you have that the gravitational force on the object, due to its weight, is given by:

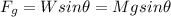`F_g=Wsin\theta=Mg sin\theta` (2)

M: mass of the ice block = 39 kg

g: gravitational constant = 9.8m/s^2

θ: angle of the incline

You calculate the angle by using the information about the distance of the incline and its height, as follow:

`sin\theta=(0.74m)/(2.8m)=0.264\\\\\theta=sin^(-1)(0.264)=15.32\°`

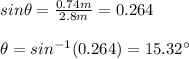
Finally, you solve the equation (1) for Fw and replace the values of all parameters:

`F_w=F_g=Mgsin\theta\\\\F_w=(39kg)(9.8m/s^2)sin(15.32\°)=101.01N`

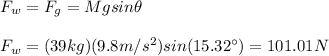
The worker's force is 101.01N

(b) The work done by the worker is given by:

`W=F_wd=(101.01N)(2.8m)=282.82J`

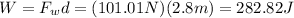
(c) The gravitational force on the block is, without taking into account the rotated system for the incline, only the weight of the ice block:

`F_g=Mg=(39kg)(9.8m/s^2)=382.2N`

The gravitational force is 382.2N

(d) The normal force is:

`N=Mgcos\theta=(39kg)(9.8m/s^2)cos(15.32\°)=368.61N`

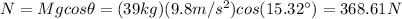
(e) The speed of the block when it slides down the incle is constant, then, by the Newton second law you can conclude that the net force is zero.