Answer:
(a) F1 = 7.19N
(b) F2 = 1.01N
Step-by-step explanation:
You have the following two forces exerted to an object:
F1: larger force
F2: weaker force
When the forces are in the same direction, to the east, the acceleration of the object is 0.919 m/s^2.
You use the Newton second law to write the following equation:
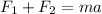 (1)
(1)
m: mass of the object = 8.93 kg
When the two forces are in opposite direction, one to the east and the other one to the west, you have the following equation (2):
 (2)
(2)
a': acceleration = 0.693 m/s^2
Then, with both equations (1) and (2) you have a 2x2 systems of equation.
You can find the values of F1 and F2 by solving the 2x2 system.
First, you sum equation (1) and (2):
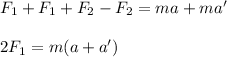 (3)
(3)
You solve the equation (3) for F1:

Next, you can replace the value of F1 into the equation (1) and you can obtain the value of F2:
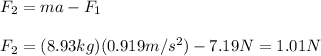
Finally, you have:
(a) The values of the larger force is 7.19N
(b) The values of the weaker force is 1.01N