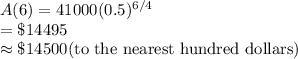Answer:
$14500
Explanation:
For a car with an initial value
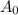 , its value, A(t) after time t for which it depreciates by period k with a decay rate of r is given is:
, its value, A(t) after time t for which it depreciates by period k with a decay rate of r is given is:
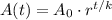
If the value of the car depreciated by
 every four years, then the value of the car at any time t is defined by the function:
every four years, then the value of the car at any time t is defined by the function:
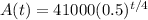
We want to determine the value of the car 6 years after it was purchased.
When t=6